概要

コンピュータシステムの理論と実装の 1 章 「ブール理論」のまとめ

内容紹介

Nand 回路を基本回路として、NOT, AND などのブール代数と、論理ゲートを構築する章。

回路を紙に書き起こすのは簡単だが、ハードウェア記述言語(HDL)の仕様で少し詰まるところがあるかも。 私は詰まりました。

論理ゲートの書き起こし

まずは使用する論理ゲートを紙に書き起こします。
作図には論理回路エディタを使用しました。

Not

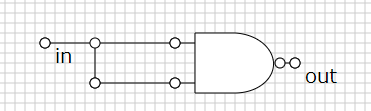NOT は NAND の両方に同一信号を流しこめばいい。

And

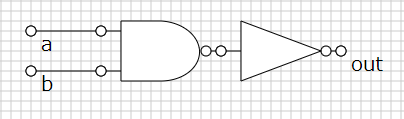NAND と先に作った NOT 回路を組み合わせて完成。

Or

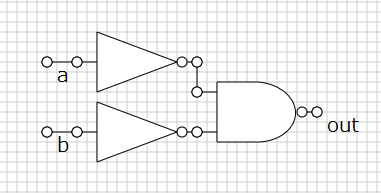発想は NAND を逆転させる感じ。ただし、出力に NOT をかけても AND 回路になる。入力に NOT をかけてあげれば完成。

Xor

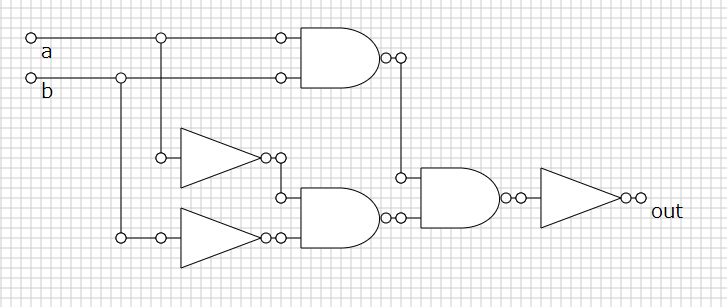a, b の対称性を使う発想。
a, b が (0, 1), (1, 0) で同じ信号を出力する回路を組んであげようとするとできる。

Mux

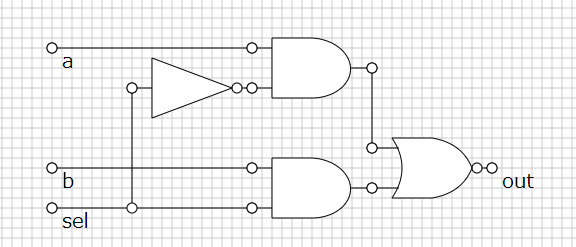sel で a, b の信号を選ぶ。 つまり sel と a, b の AND を出力する回路を組めばいい。

DMux

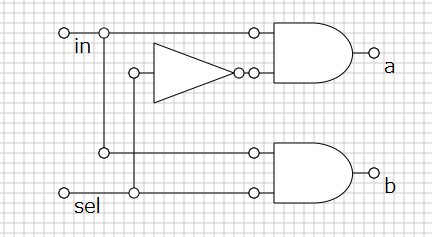sel に信号が入っていない時に a に出力するという点に気を付けて。

多ビット Not, And, Or

多ビットについてはすでに組んだ回路を並べるだけでできます。

多入力 Or

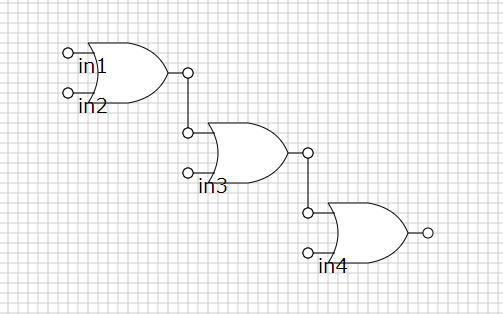本当に困難でいいの？ と疑問を持ちますがいいのです。
すでに組んだ OR を 8 個接続するだけです。

Mux4Way16

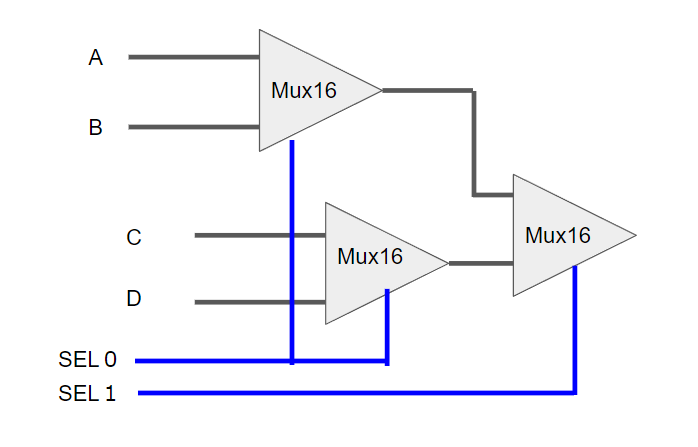sel を 1 つずつ処理すればいい。 処理順はどちらでもできるが、0 から順に処理することにしました。

Mux8Way16

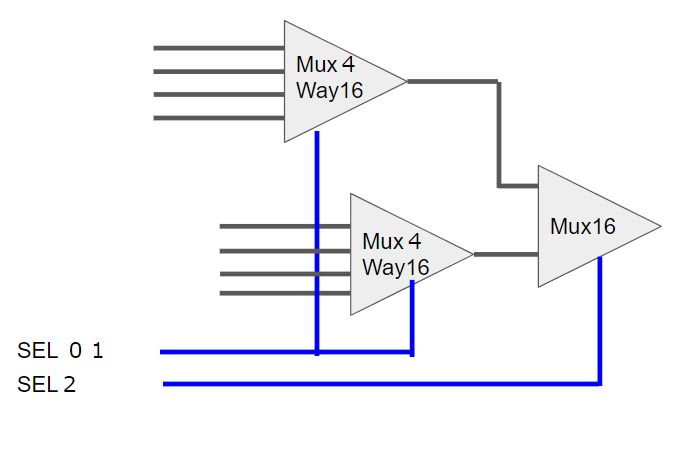Mux4 Way16 を組み合わせれば完成。
HDL で記述するのが面倒なだけで難しくはない。

DMux4Way

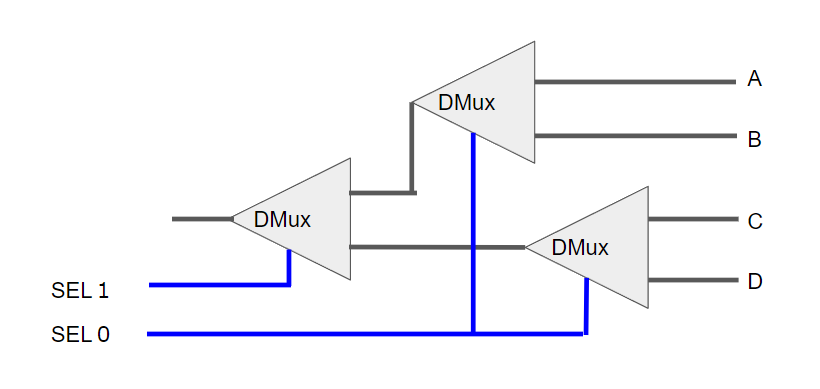Sel0, 1 を逆にしないように注意。

DMux8Way

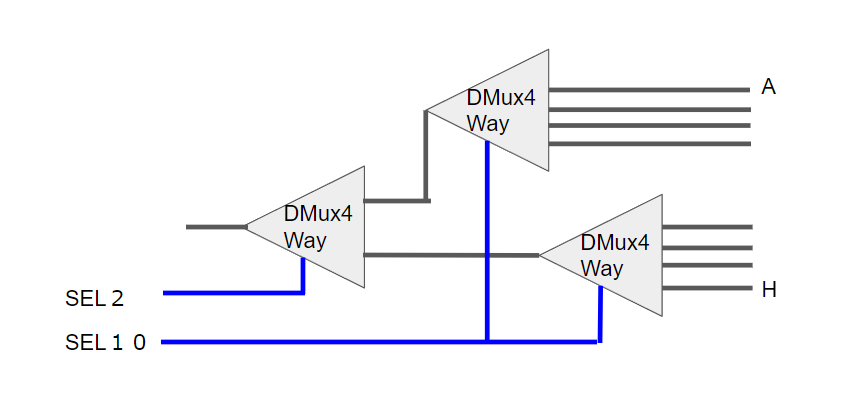
HDL の注意点

HDL で私がハマった点です。

• HDL は両閉区間。 python や C は半開区間なので、sel の指定時などに注意。